POL 304: Using Data to Understand Politics and Society

class: center, middle, inverse, title-slide

.title[
# POL 304: Using Data to Understand Politics and Society
]
.subtitle[
## Intro to Network Analysis
]
.author[
### Olga Chyzh [www.olgachyzh.com]
]

---

## Today's Class

1. Definitions. What is network analysis?
 
 2. Network data
 
 3. Network features and measurements
 
 4. An application: modeling contagion

---

## Would You Win $1,000,000?

Suppose you are playing the following game:

If you can get all your friends to meet you at the entrance to the ROM in exactly 1 hour, you will win $1,000,000. The catch is that you can only contact one friend, and not all your friends know each other. Which friend would you call and why?

---

| Sender | Receiver |
|----------|----------|
| 1    | 2, 3   |
| 2    |1, 3, 4, 5   |
| 3    | 1, 2, 4, 5  |
| 4    |2, 3, 5, 7  |
| 5    | 2, 3, 4, 6, 7   |
|6     |5, 7, 8   |
|  7    | 4, 5, 6   |
| 8    |6, 9, 12   |
|9    | 8, 10   |
| 10   |9  |
| 11   | 12  |
| 12   | 8, 11, 13, 14, 15, 16  |
| 13   | 12 |
| 14   | 12 |
| 15   | 12 |
| 16   | 12 |

---
## Visualization of the Friends Network

---
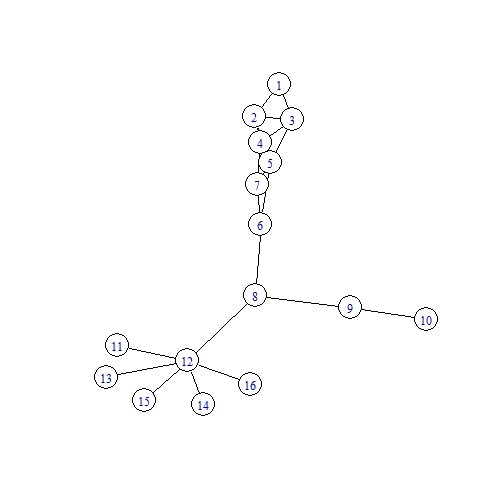
## Discussion

- What criterion helps spread the message in the fewest possible steps?

- What are social science applications of this game?

---

## Why Do We Need Network Analysis?
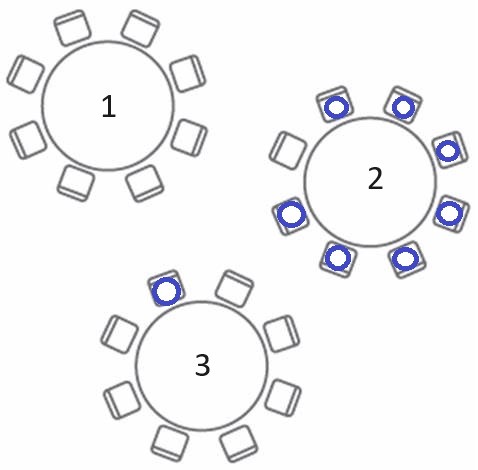
Suppose you walked into a dining room that hosts a luncheon at a conference you are currently attending. What table would you sit at?

---
class: inverse, middle, center

# Network Analysis: Formal Definitions

---

## What is a network (i.e., a graph)?

A set of **nodes** and **relation(s)** defined on them

<img src="images/madmen.png" width="400px" style="display: block; margin: auto;" />
---

## Defining a Network: What's a node?

- A <span style="color:DarkCyan">**node**</span> can be defined as an entity that can form relations with other entities.

**Synonyms**:

- actor: from sociometry, common terminology in sociology and psychology
- vertex: from graph theory (i.e., math), common terminology in mathematics and physics

Term node is common in statistics and applied sciences outside of soc and psych.
---
## Examples of Nodes

- Individuals (Mad Men characters, legislators, terrorists)

- Families

- Organizations, Human Rights NGOs

- Countries
---
## Defining Network: What's a tie?

- A <span style="color:DarkCyan">**relation/tie**</span> defines the existence of an attribute relating nodes.

**Synonyms**:

- link: common in computer science (e.g., huge lit on “Link Prediction”) and social sciences
- edge: graph theoretic terminology common in physics and math, but also elsewhere

**Ties can have characteristics**:

- Weight
- Qualitative attributes
- Direction
---
## Examples of Ties

- Romantic relationship, marriage, friendship

- Business relationship

- Cooperation/conflict
---

## Network graphs can reveal important structures

<div class="figure" style="text-align: center">
<img src="images/p1.png" alt=" " width="49%" height="10%" /><img src="images/p2.png" alt=" " width="49%" height="10%" />
<p class="caption"> </p>
</div>
---
## Adolescent romantic and sexual networks

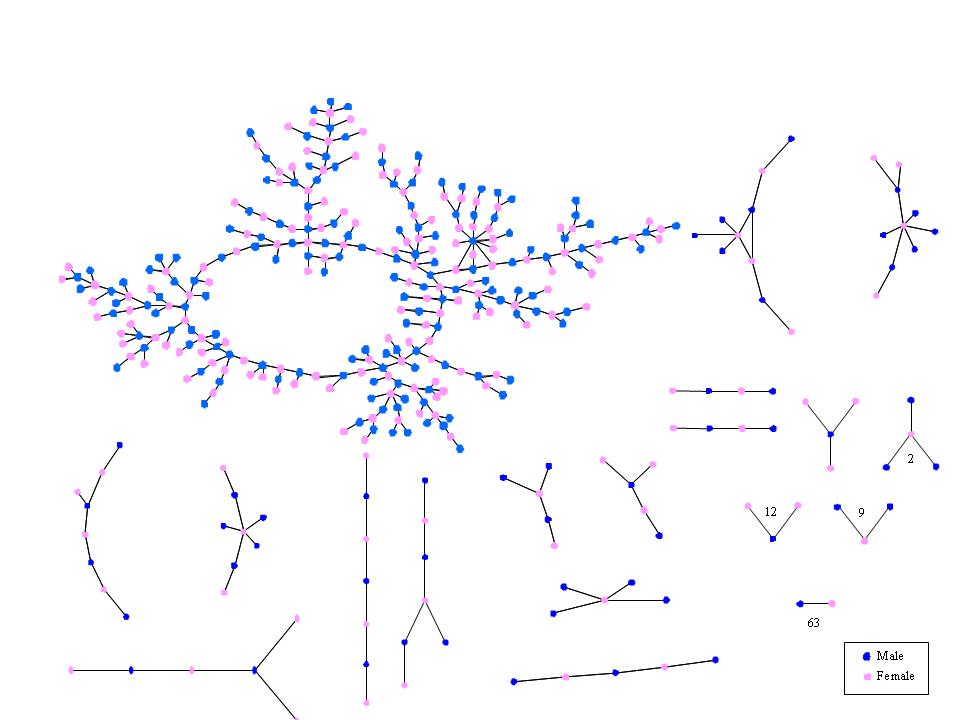<img src="images/jefferson.jpg" width="600px" style="display: block; margin: auto;" />
**Bearman, Moody and Stovel**
---
## Adolescent Social Structure by **Jim Moody**
<img src="images/schoolGrade.png" width="600px" style="display: block; margin: auto;" />

---
## Adolescent Social Structure by **Jim Moody**
<img src="images/schoolRace.png" width="600px" style="display: block; margin: auto;" />

---
class: inverse, middle, center

# Other Important Definitions

---
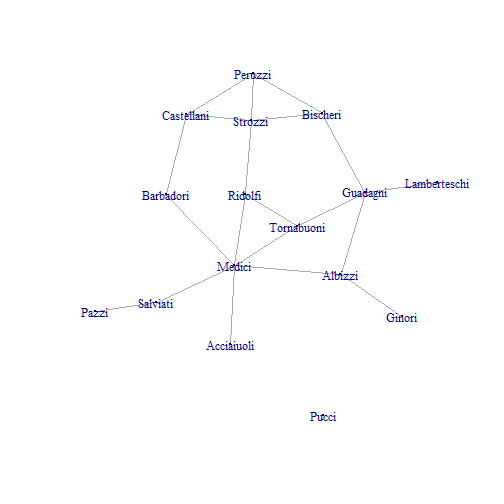
## An Adjacency Matrix 
Network data are often stored in the form of *adjacency matrices* whose `$ij^{th}$` element represents the relationship between nodes `$i$` and `$j$`.

```
##              Acciaiuoli Albizzi Barbadori Bischeri Castellani Ginori
## Acciaiuoli            0       0         0        0          0      0
## Albizzi               0       0         0        0          0      1
## Barbadori             0       0         0        0          1      0
## Bischeri              0       0         0        0          0      0
## Castellani            0       0         1        0          0      0
## Ginori                0       1         0        0          0      0
## Guadagni              0       1         0        1          0      0
## Lamberteschi          0       0         0        0          0      0
## Medici                1       1         1        0          0      0
## Pazzi                 0       0         0        0          0      0
## Peruzzi               0       0         0        1          1      0
## Pucci                 0       0         0        0          0      0
## Ridolfi               0       0         0        0          0      0
## Salviati              0       0         0        0          0      0
## Strozzi               0       0         0        1          1      0
## Tornabuoni            0       0         0        0          0      0
```

---

## Network Measures: Centrality

- Centrality measures help understand:

+ **"Which node is the most important or central in this network?"**
  
  + What do you mean by "important"?
  
  + What do you mean by "center"?
  
  + Definition of "center" varies by context/purpose
    
    + The power a person holds in an organization may be inversely proportional to the number of keys on their keyring 
      
      + A janitor has keys to every office, and no power
      
      + The CEO does not need a key: people always open the door for her
---

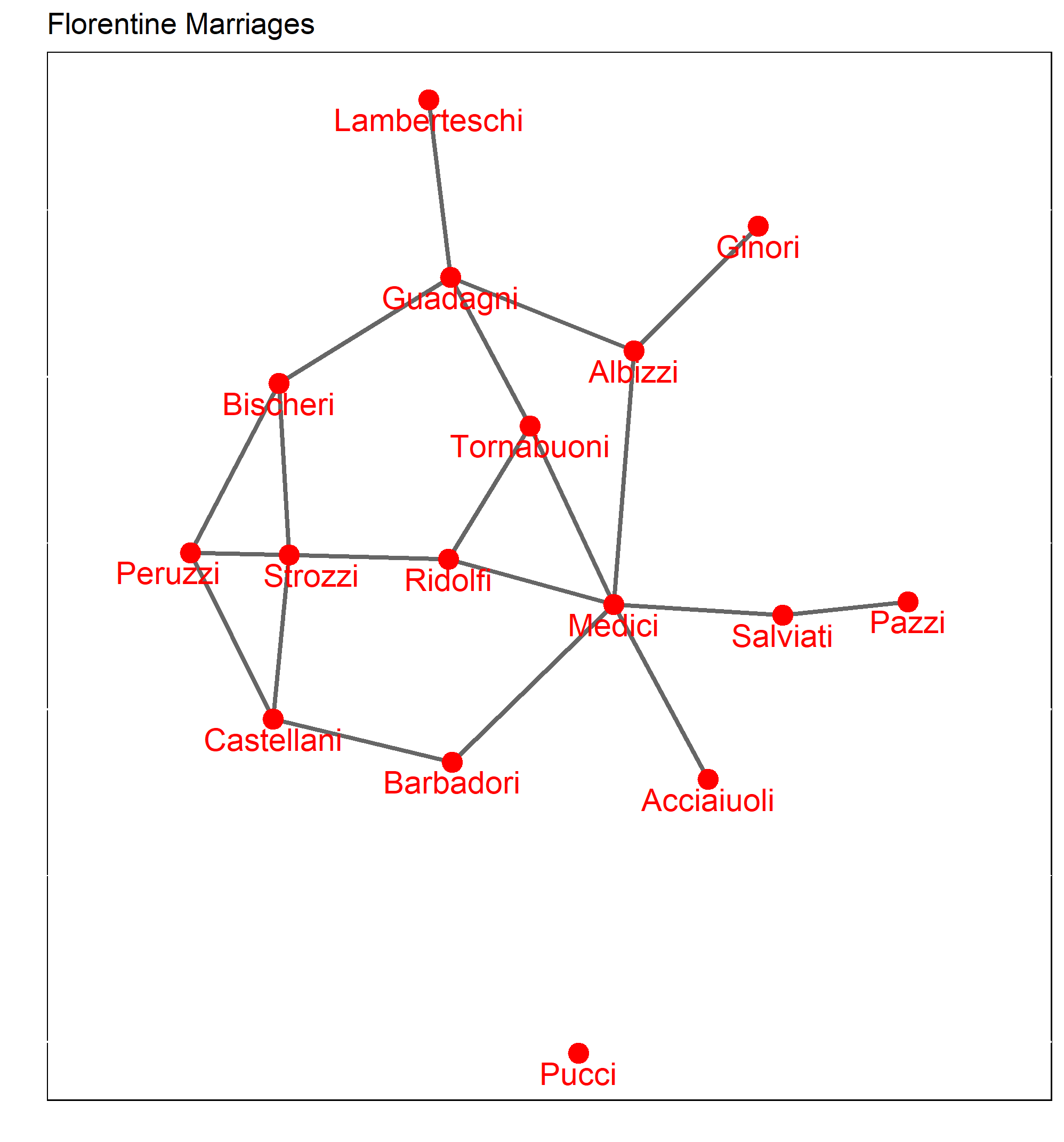
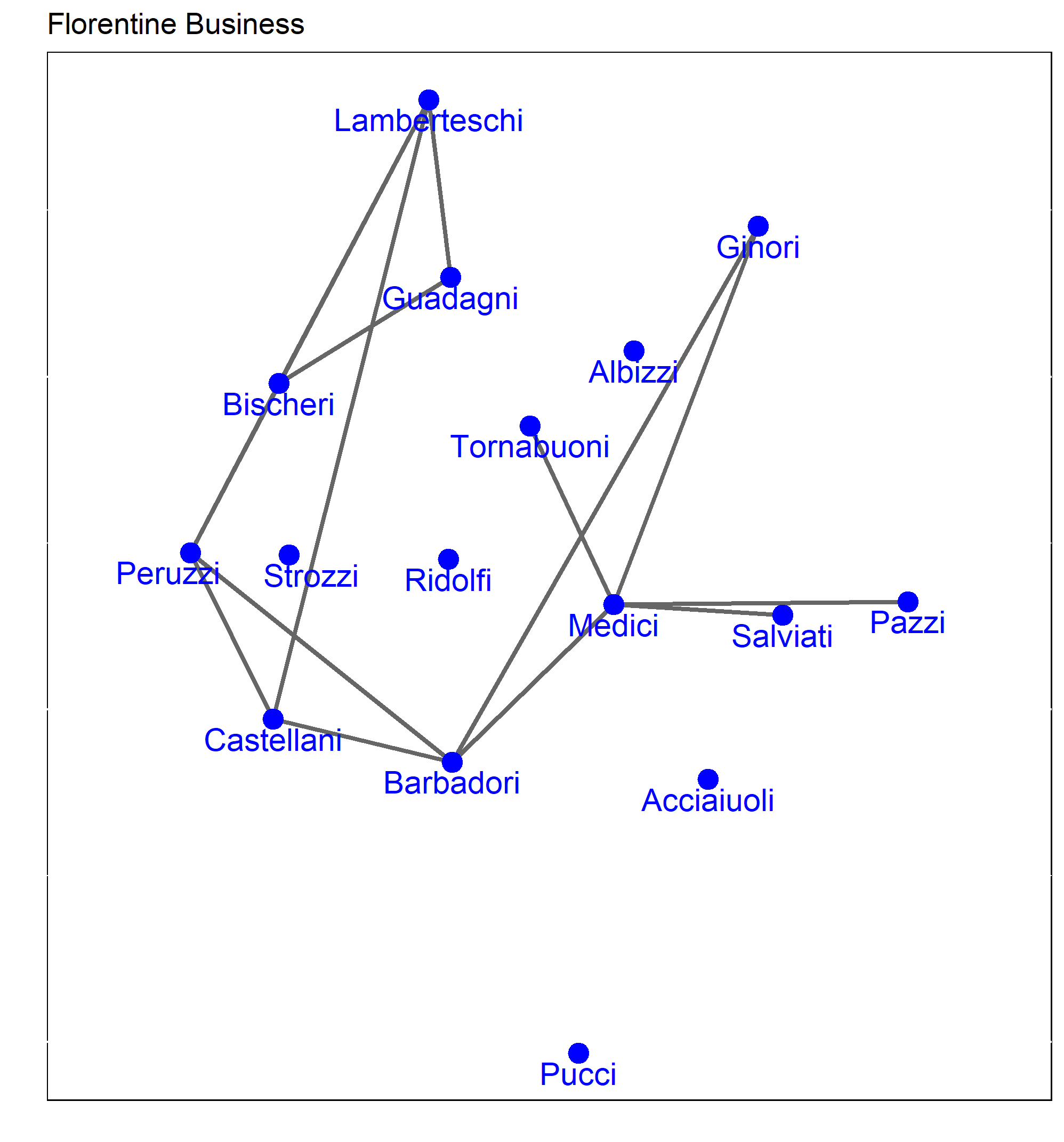
## Florentine Families

Who looks central?

---
## Network Measures: Degree Centrality

- **Idea**: The nodes with more connections to others are more central

- How to  measure: node `$i$`'s degree is the sum of its direct ties.

- Though simple, degree is often a highly effective measure of the influence or importance of a node
  
  + In many situations, people with more connections tend to have more power

- Examples where this might be useful?

---

## Florentine Families: an Adjacency Matrix

How would you calculate Albizzi's degree centrality?

---

## Network Measures: The Shortest Path

- The (geodesic) distance: `$d_{i,j}$` is the minimal path length from `$i$` to `$j$`.

- Example: Can identify and count all nodes within the shortest path of `$2$` from *i*

- Useful for modeling contagion, or spread of information.

---

## The Shortest Path: Calculation

Let `$A_{ij}$` represent the adjacency matrix associated with a network of interest. It turns out that the `$ij^{th}$` element of `$A^2$` will give you the number of the shortest paths of length 2 between `$i$` and `$j$`.

.pull-left[

`$A$`

```
##    1 2 3 4 5 6 7 8 9 10
## 1  0 0 0 0 0 0 0 0 1  0
## 2  0 0 0 0 0 1 1 0 1  0
## 3  0 0 0 0 1 0 0 0 1  0
## 4  0 0 0 0 0 0 1 0 0  0
## 5  0 0 1 0 0 0 0 0 0  0
## 6  0 1 0 0 0 0 0 0 0  0
## 7  0 1 0 1 0 0 0 1 0  0
## 8  0 0 0 0 0 0 1 0 0  0
## 9  1 1 1 0 0 0 0 0 0  0
## 10 0 0 0 0 0 0 0 0 0  0
```
]

.pull-right[
`$A^2$`

```
##    1 2 3 4 5 6 7 8 9 10
## 1  0 1 1 0 0 0 0 0 0  0
## 2  1 0 1 1 0 0 0 1 0  0
## 3  1 1 0 0 0 0 0 0 0  0
## 4  0 1 0 0 0 0 0 1 0  0
## 5  0 0 0 0 0 0 0 0 1  0
## 6  0 0 0 0 0 0 1 0 1  0
## 7  0 0 0 0 0 1 0 0 1  0
## 8  0 1 0 1 0 0 0 0 0  0
## 9  0 0 0 0 1 1 1 0 0  0
## 10 0 0 0 0 0 0 0 0 0  0
```
]

---

## Matrix Multiplication Refresher

---
class: inverse, middle, center
# Lab: A Network Model fo Contagion

---
## Example: High-School Friendships

1. Open and explore the data

2. Notice that the data contain 2 waves (fall and spring), each stored as an adjacency matrix.

```r
library(sna)
data(coleman)
coleman[1,1:10,1:10]
```

```
##    1 2 3 4 5 6 7 8 9 10
## 1  0 0 0 0 0 0 0 0 0  0
## 2  0 0 0 0 0 0 0 0 0  0
## 3  0 0 0 0 0 0 0 0 1  0
## 4  0 0 0 0 1 0 0 0 0  0
## 5  0 0 0 0 0 0 0 0 0  0
## 6  0 0 0 0 0 0 0 0 0  0
## 7  0 0 0 0 0 0 0 0 0  0
## 8  0 0 0 0 0 0 0 0 0  0
## 9  0 0 0 0 0 0 0 0 0  0
## 10 0 0 0 0 0 0 0 0 0  0
```

---
## Make a Network Visualization

Convert to an `igraph` object:

```r
library(igraph)
ggraph<-graph_from_adjacency_matrix(coleman[1,,], mode="undirected", diag=FALSE)
plot(ggraph, vertex.color="black", vertex.size=5, vertex.label=NA)
```

---
## Calculate Degree Centrality for Each Node

```r
degree.cent <- igraph::degree(ggraph)
degree.cent
```

```
##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 
##  5  2  2  4  3  3  1  2  6  1  5  4  6  4  3  4  3  5  6  8 12 10  9  1  0  6 
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 
##  4  2  3  2  4  5  5  2  4  5  3  7  5  6  6  6 10  1  5  4  5  6  6  7  6  7 
## 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 
##  6 10  8  3  6  3  4  5  4  5  6  5  6  7  6 10  7 10 10  0  0
```

---

## Visualize Information Spread

1. Select the first individual to share the information with (the seed).

2. Color the seed node red.

```r
V(ggraph)$color <- ifelse(V(ggraph)$name == 21, "red", "grey")
plot(ggraph)
```

---

## Shortest Path of 1

```r
neighbors(ggraph,21)
```

```
## + 12/73 vertices, named, from 1a6ab0a:
##  [1] 1  2  9  12 13 14 20 22 38 51 54 55
```

```r
V(ggraph)$color <- ifelse(V(ggraph)$name %in% neighbors(ggraph,21), "pink", "grey")
V(ggraph)$color[V(ggraph)$name == 21]<- "red"
plot(ggraph)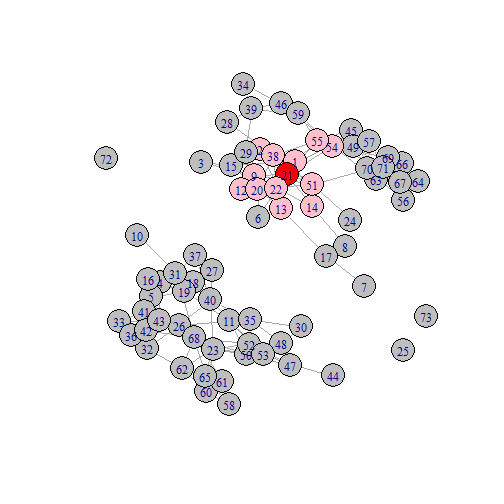
```

---

## Shortest Path of 2

1. Convert `ggraph` to an adjacency matrix, A.

2. The elements of `$A^2$` will give you the number of shortest paths of length 2 between `$i$`'s and each other node.

3. Select nodes that have 1 or more shortest path of length 2 to node 21.

```r
mynet<-as.matrix(igraph::as_adj(ggraph))
mynet2<-mynet%*%mynet
diag(mynet2)<-0 #a node cannot be connected to itself
neighbors2<-names(mynet2[21,][mynet2[21,]>0])
neighbors2
```

```
##  [1] "1"  "2"  "3"  "6"  "8"  "9"  "12" "13" "14" "15" "17" "20" "22" "24" "28"
## [16] "29" "38" "45" "46" "49" "51" "54" "55" "57" "59" "63" "69" "70" "71"
```

---

```r
V(ggraph)$color <- ifelse(V(ggraph)$name %in% neighbors2, "mistyrose", "grey")
V(ggraph)$color[V(ggraph)$name %in% neighbors(ggraph,21)]<- "pink"
V(ggraph)$color[V(ggraph)$name == 21]<- "red"
plot(ggraph, vertex.label=NA)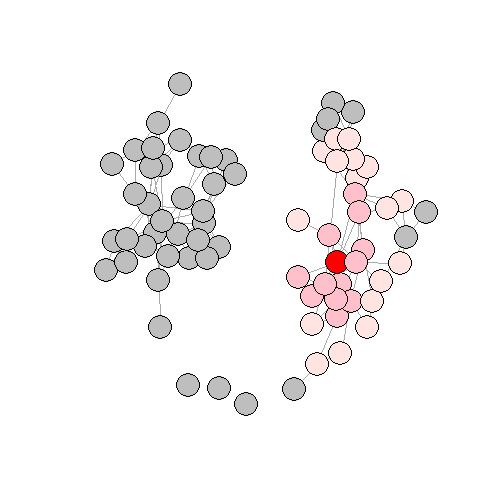
```

---

## Your Turn

Below if the code to create the hypothetical friendship network used in the opening example.

- Model the spread of information in this network using "12", "6", and "8" as the seed.

```r
el <- matrix( c("1", "2", "1", "3","2","3","3","5","2","4","2","5","3","4","4","5","4","7","6","5","5","7","6","7","6","8", "8","9","9","10", "8","12", "11","12",  "12","13","12","14","12","15","12","16"), nc = 2, byrow = TRUE)
g<-graph_from_edgelist(el, directed=F)
```